We use most of the structural and electrophysiological features introduced in the Allen Cell Types Database [30] to characterize both biological neurons and neuron models. Table 1 lists the structural attributes and their definitions. In the Allen Cell Types Database, the structural attributes (S${}_1$ to S${}_{16}$) are defined based on the detailed cell morphology obtained via tissue sections in situ and reconstructions of individual neurons [31]. The electrophysiological features are based on information about spiking behaviors obtained from whole-cell patch-clamp recordings with three types of stimulus protocols, including long square current, ramp current, and short square current injections [32]. The electrophysiological features are classified into the spike train-related features (ET${}_1$ to ET${}_4$) and spike shape-related features (ES${}_1$ to ES${}_{36}$), as summarized in Supplementary Table 1 in supplementary material.

The neuron models for three primary cells in the hippocampus, i.e., the pyramidal cell in Cornu Ammonis 1 (CA1), that in CA3, and granule cell in the dentate gyrus (DG), are systemically analyzed (Fig. 1). These models were developed by Vetter et al. (ModelDB accession 7907) [33] to examine the effects of dendrite structures on the efficacy of the forward/backward propagation of action potentials; the models describe realistic structures via three-dimensional morphological reconstruction of biological neurons [34, 35, 36]. All dendrites are divided into compartments with a maximum length of 7 mm. Two Hodgkin–Huxley-type conductances (g${}_{Na}$ and g${}_K$) are inserted into the soma and dendrites at uniform densities. The model is tuned by attaching a synthetic axon. The uniform passive parameters of the model are R${}_i$ = 150 $\mathrm{\Omega }$$\cdot$cm, C${}_m$ = 1 $\mu$F/cm${}^2$, and R${}_m$ = 12 k$\mathrm{\Omega }$$\cdot$cm${}^2$. The standard values for g${}_{N\mathit{}a}$ and g${}_K$ are 35 and 30 pS/mm${}^2$, respectively. Channel kinetics and densities are adjusted at temperature 37 ${}^{\circ }$C.

Fig. 1.

An information-theoretic framework for evaluating neural information processing of models for hippocampal neurons. (a) Illustration for the CA1 pyramidal neuron. Two synaptic inputs (blue and red arrows) are presented on the apical dendrite. The synaptic inputs are triggered by hidden states x${}_{\mathrm{1}}$ and x${}_{\mathrm{2}}$, with coherence $\alpha$ between them. The output spike train is measured at the soma (green arrow). Exemplary patterns of the hidden state and output spike train are displayed above the corresponding arrows; that of the excitatory postsynaptic potential (EPSP) in the upper right (red curve). Mutual information I(x${}_i$, y) between x${}_i$ (i = 1 or 2) and output y is calculated. Schematics for the (b) CA3 pyramidal neuron and (c) DG granule cell.

The synaptic conductance is described in terms of the dynamics of ionotropic glutamate receptors such as the $\alpha$-amino-3-hydroxy-5-methyl-4-isoxazole propionic acid (AMPA) receptor, based on the work by Vetter et al. [33]. The dynamic behaviors of receptors are fitted with biexponential function with the exponential rise and decay time constants of 0.2 and 1.7 ms, respectively; a reversal potential of the conductance is set to 0 mV and a maximum synaptic conductance to 50 nS. This allows obtaining the time evolution of the receptor conductance to evaluate the information processing at the synapse level.

We modify the three primary structural factors (i.e., dendritic length, diameter, and the number of branches) to test if these factors can influence neural dynamics and information processing. The lengths or diameters of all dendritic compartments in the model are multiplied by the same value (e.g., 2-fold increase or 0.5-fold decrease). The number of branches is varied in the following manner: either new branches with fixed diameter and length (e.g., 0.5 $\mu$m in diameter and 156 $\mu$m in length) are added to the bifurcation sites (i.e., nodes of a parent branch segment where the branch is divided into two daughter branches) of the parent branches, or the shorter branches on the randomly chosen bifurcation sites are deleted. All simulations have been performed via the NEURON program (v7.8, https://neuron.yale.edu/) [37, 38] with a time step of 0.01 ms.

Mutual information between a presynaptic binary hidden state and the axonal output spike train provides a useful tool for characterizing neural information processing of the neuron models. We extend the information-theoretic framework, first suggested by Denève and colleagues [39, 40, 41, 42, 43], to include multiple synapses and hidden states, similarly to our previous work [44]. The binary hidden state of a neuron represents a stimulus that appears and disappears randomly. For instance, the stimulus may correspond to a bar with a given orientation in a visual receptive field or a sound with a preferred frequency. Each of the hidden states x${}_{\mathrm{1}}$ and x${}_{\mathrm{2}}$ takes the value 1 or 0 for the state on or off, respectively. The coherence between x${}_{\mathrm{1}}$ and x${}_{\mathrm{2}}$ is measured by $\alpha$ in the range [0, 1]: $\alpha$ vanishes for the two states behaving independently while it is set equal to unity for the two fully synchronized.

The binary hidden states follow a Markov process with the composite hidden state (x${}_{\mathrm{1}}$, x${}_{\mathrm{2}}$) that changes according to the transition probability p(x${}_{\mathrm{1}}$x${}_{\mathrm{2}}$$\to$ x${}^{\mathrm{\prime }}$${}_{\mathrm{1}}$x${}^{\mathrm{\prime }}$${}_{\mathrm{2}}$) from (x${}_{\mathrm{1}}$, x${}_{\mathrm{2}}$) to (x${}^{\mathrm{\prime }}$${}_{\mathrm{1}}$, x${}^{\mathrm{\prime }}$${}_{\mathrm{2}}$):

(1)
$p(00\to 00)={(1-p_{\text{on}})}^2+(p_{\text{on}}-p_{\text{on}}^2)\alpha ,$
$p(00\to 01)=p(00\to 10)=(p_{\text{on}}-p_{\text{on}}^2)(1-\alpha ),$
$p(00\to 11)=p_{\text{on}}^2+(p_{\text{on}}-p_{\text{on}}^2)\alpha ,$
$p(01\to 00)=p(10\to 00)=(1-p_{\text{on}})p_{\text{off}},$
$p(01\to 01)=p(10\to 10)=(1-p_{\text{on}})(1-p_{\text{off}}),$
$p(01\to 10)=p(10\to 01)=p_{\text{on}}{p}_{\text{off}},$
$p(01\to 11)=p(10\to 11)=p_{\text{on}}(1-p_{\text{off}}),$
$p(11\to 00)=p_{\text{off}}^2+(p_{\text{off}}-p_{\text{off}}^2)\alpha ,$
$p(11\to 01)=p(11\to 10)=(p_{\text{off}}-p_{\text{off}}^2)(1-\alpha ),$
$p(11\to 11)={(1-p_{\text{off}})}^2+(p_{\text{off}}-p_{\text{off}}^2)\alpha ,$

where p ${}_{o\mathit{}n}$ = r${}_{o\mathit{}n}$$\delta$t and p ${}_{o\mathit{}f\mathit{}f}$ = r${}_{o\mathit{}f\mathit{}f}$$\delta$t with the simulation time step $\delta$ t and rate parameters r${}_{o\mathit{}n}$ and r${}_{o\mathit{}f\mathit{}f}$. The synaptic inputs triggered by hidden state x${}_i$ follow a Poisson process with rates q${}_{o\mathit{}n}$ and q${}_{o\mathit{}f\mathit{}f}$ for x${}_i$ = 1 and 0, respectively. The postsynaptic spike train y(t) is defined as follows: It takes the value unity (y = 1) or vanishes (y = 0) according to whether or not the membrane potential of the soma crosses 0 mV in the positive direction. For the simulations with a single hidden state x, the transition probability is the marginal distribution of Eqn. 1.

The mutual information I(x${}_i$; y) between the hidden state x${}_i$ and the postsynaptic spike train y is given by

(2)
$I(x_i;y)=H\left(x_i\right)-H\left(x_i\mid y\right),$

where the entropy H(x${}_i$) of x${}_i$ is estimated as

(3)
$H\left(x_i\right)=-⟨x_i⟩{\log }_2⟨x_i⟩-\left(1-⟨x_i⟩\right){\log }_2\left(1-⟨x_i⟩\right)$

and the conditional entropy

(4)
$\mathrm{H}({\mathrm{x}}_{\mathrm{i}}\mid \mathrm{y})=-⟨{\mathrm{x}}_{\mathrm{i}}{\log }_2\mathrm{p}({\mathrm{x}}_{\mathrm{i}}=1\mid \mathrm{y})+(1-{\mathrm{x}}_{\mathrm{i}}){\log }_2\mathrm{p}({\mathrm{x}}_{\mathrm{i}}=0\mid \mathrm{y})⟩$ $=-⟨{\mathrm{x}}_{\mathrm{i}}{\log }_2\mathrm{p}({\mathrm{x}}_{\mathrm{i}}=1\mid \mathrm{y})+(1-{\mathrm{x}}_{\mathrm{i}}){\log }_2[1-\mathrm{p}({\mathrm{x}}_{\mathrm{i}}=1\mid \mathrm{y})]⟩$

with angled brackets denoting time averages. The conditional probability p(x${}_i$$|$ y) is computed by calculating the posterior log-likelihood of the hidden state being on (x${}_i$ = 1), based on the input history:

(5)
$L_i(t)={\log }_2{\displaystyle \frac{p(x_i=1\mid y)}{p(x_i=0\mid y)}}.$

We estimate the posterior log-likelihood L${}_i$ via the differential equation:

(6)
${\displaystyle \frac{{\mathrm{dL}}_{\mathrm{i}}}{\mathrm{dt}}}={\mathrm{r}}_{\mathrm{on}}\left(1+\exp \left[-{\mathrm{L}}_{\mathrm{i}}\right]\right)-{\mathrm{r}}_{\mathrm{off}}\left(1+\exp \left[{\mathrm{L}}_{\mathrm{i}}\right]\right)+\mathrm{w}\delta [\mathrm{y}(\mathrm{t})-1]+\theta$

where w$\equiv$ log(f${}_{o\mathit{}n\mathrm{,}\text{𝑖}}$/f${}_{o\mathit{}f\mathit{}f\mathrm{,}\text{𝑖}}$) and $\theta$$\equiv$ f${}_{o\mathit{}n\mathrm{,}\text{𝑖}}$–f${}_{o\mathit{}f\mathit{}f\mathrm{,}\text{𝑖}}$ with the mean postsynaptic firing rates f${}_{o\mathit{}n\mathrm{,}\text{𝑖}}$ and f${}_{o\mathit{}f\mathit{}f\mathrm{,}\text{𝑖}}$ for x${}_i$ = 1 and 0, respectively. The Dirac delta function $\delta$[y(t)–1] produces a discontinuous jump when the postsynaptic neuron fires. Eqs. (5) and (6) give p(x${}_i$=1$|$ y), which is used for calculating Eq. (4) and thus I(x${}_i$; y).

Fig. 2 displays Pearson correlation coefficients between the structural and electrophysiological features (i.e., spike shape-related features, denoted as ES${}_i$ for i = 1, …, 36 and spike train-related ones, ET${}_i$ for i = 1, …, 4) of biological neurons in the Allen Cell Types Database. While the average single-neuron structural features, i.e., ‘average local bifurcation angle S${}_1$’, ‘average contraction S${}_2$’, ‘average diameter S${}_3$’, and ‘average parent-daughter ratio S${}_4$’, are not strongly correlated with either spike shape- or spike train-related features, the non-averaged structural features (S${}_5$ to S${}_{16}$) generally exhibit relatively high positive/negative correlations with the electrophysiological features.

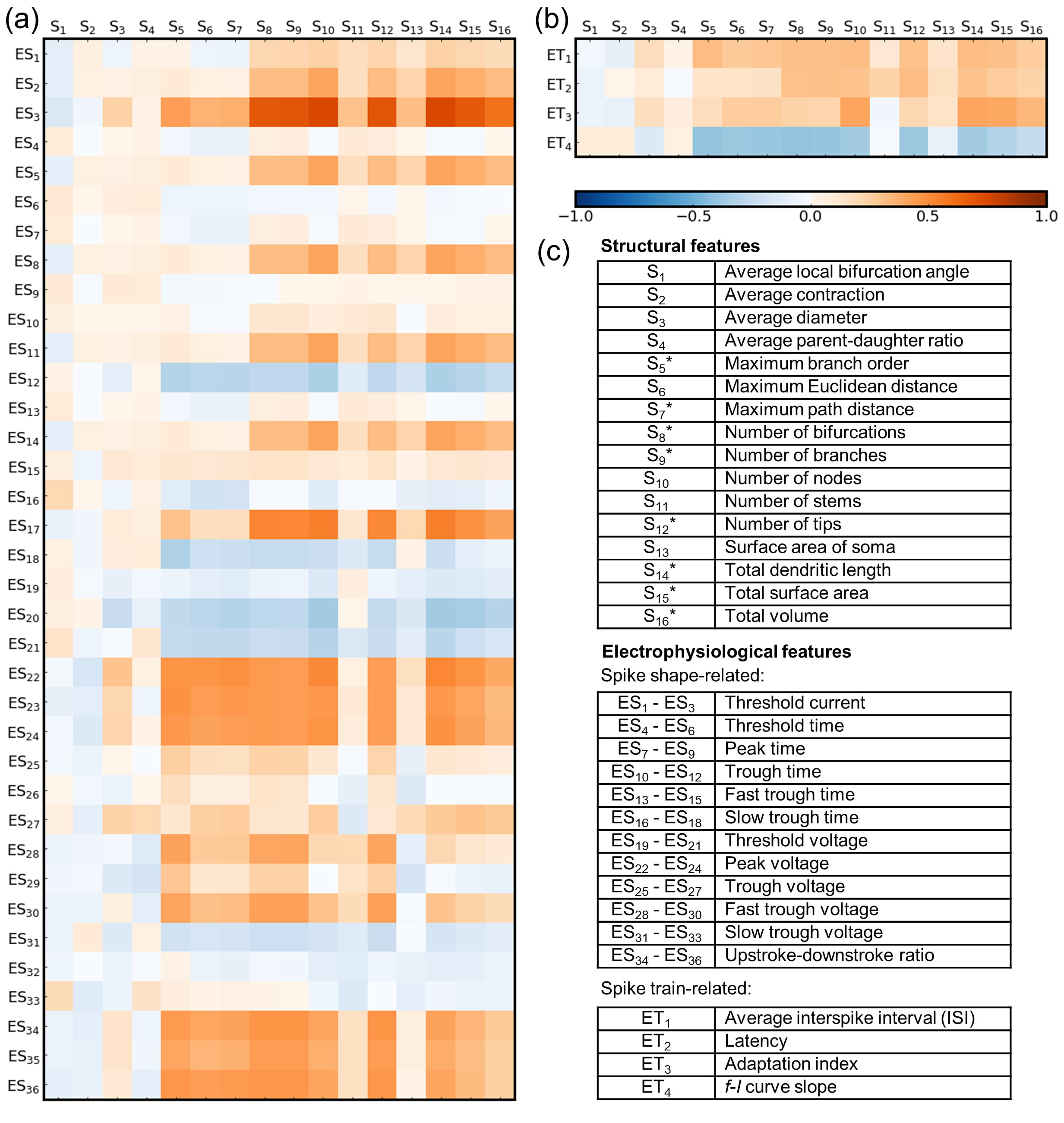Fig. 2.

Correlations between the structural and electrophysiological features of biological neurons in the Allen Cell Types Database. (a) Pearson correlation coefficients between structural features (S${}_1$ to S${}_{16}$) and electrophysiological features regarding spike shape (ES${}_1$ to ES${}_{36}$) and (b) spike train (ET${}_1$ to ET${}_4$). The value and sign of the Pearson correlation coefficient are color-coded; the color scale bar is presented at the bottom of (b). (c) List of structural and electrophysiological features considered in this study. Each of the spike shape-related features has three different values according to the current injection modes. For instance, the ‘threshold current’ is denoted as ES${}_1$ when the output spike is measured upon a long square current injection, ES${}_2$ with a ramp injection, and ES${}_3$ for a short square mode. Other spike shape-related features are also displayed in the same order. Eight structural features (S${}_5$, S${}_7$, S${}_8$, S${}_9$, S${}_{12}$, S${}_{14}$, S${}_{15}$, and S${}_{16}$) taken as the primary set to characterize neuron models are marked with asterisks (*). See Table 1 in Methods for detailed descriptions of the structural features and Supplementary Table 1 in the supplementary material for electrophysiological features.

The ‘threshold currents (ES${}_1$ to ES${}_3$)’ are positively correlated with most of the non-averaged structural features (S${}_5$ to S${}_{16}$). In particular, the correlations are much higher with the short square input currents (with the Pearson correlation coefficients ranging from 0.30 to 0.75 for ES${}_3$), compared with the long square (–0.06 to 0.24 for ES${}_1$) or ramp (0.03 to 0.41 for ES${}_2$) modes (Fig. 2a). Several features such as ‘threshold time (ES${}_5$)’, ‘peak time (ES${}_8$)’, ‘trough time (ES${}_{11}$)’, ‘fast trough time (ES${}_{14}$)’, and ‘slow trough time (ES${}_{17}$)’ have positive correlations with the structural features only when the ramp current injection is applied (Fig. 2a). Upon all three injection types (i.e., long square, ramp, and short square modes), ‘peak voltages (ES${}_{22}$ to ES${}_{24}$)’ and ‘upstroke-downstroke ratios (ES${}_{34}$ to ES${}_{36}$)’ are positively correlated with most of the structural features. In contrast, ‘threshold voltages (ES${}_{19}$ to ES${}_{21}$)’ are negatively correlated with the structural features for all the input types. For the spike train-related features, ‘average interspike interval (ET${}_1$)’, ‘latency (ET${}_2$)’, and ‘adaptation index (ET${}_3$)’ are positively correlated with the structural features, but the ‘I-f curve slope (ET${}_4$)’ is negatively correlated.

Overall, among the non-averaged features (S${}_5$ to S${}_{16}$), the following features exhibit relatively higher correlations with the above-mentioned electrophysiological features: ‘maximum branch order (S${}_5$)’, ‘maximum Euclidean distance (S${}_6$)’, ‘maximum path distance (S${}_7$)’, ‘number of bifurcations (S${}_8$)’, ‘number of branches (S${}_9$)’, ‘number of nodes (S${}_{10}$)’, ‘number of tips (S${}_{12}$)’, ‘total dendritic length (S${}_{14}$)’, ‘total surface area (S${}_{15}$)’ and ‘total volume (S${}_{16}$)’. However, ‘maximum Euclidean distance (S${}_6$)’ and ‘number of nodes (S${}_{10}$)’ may not be defined in the multi-compartment neuron models used in the present study. Accordingly, the eight structural features (S${}_5$, S${}_7$, S${}_8$, S${}_9$, S${}_{12}$, S${}_{14}$, S${}_{15}$, and S${}_{16}$, each marked with an asterisk (*) in Fig. 2c) are considered as the primary set for characterizing neuronal structure in most analyses.

Fig. 3 illustrates that the eight primary structural features (i.e., S${}_5$, S${}_7$, S${}_8$, S${}_9$, S${}_{12}$, S${}_{14}$, S${}_{15}$, and S${}_{16}$) are highly correlated with the electrophysiological features. Each panel displays the relationship between each structural feature and its most strongly correlated partner. Most structural features have the highest Pearson correlation coefficient values for ES${}_3$ (i.e., Threshold current to evoke action potentials upon short square input) except S${}_5$ and S${}_7$; S${}_5$ and S${}_7$, which exhibit the highest values with ES${}_{23}$ (Peak voltage upon ramp input) and ES${}_{22}$ (Peak voltage upon long square input), respectively. The highest Pearson correlation value amounts to 0.75 for the case between S${}_{14}$ and ES${}_3$ (Fig. 3f). The full list of Pearson correlation values is presented in Supplementary Table 2 in the supplementary material.

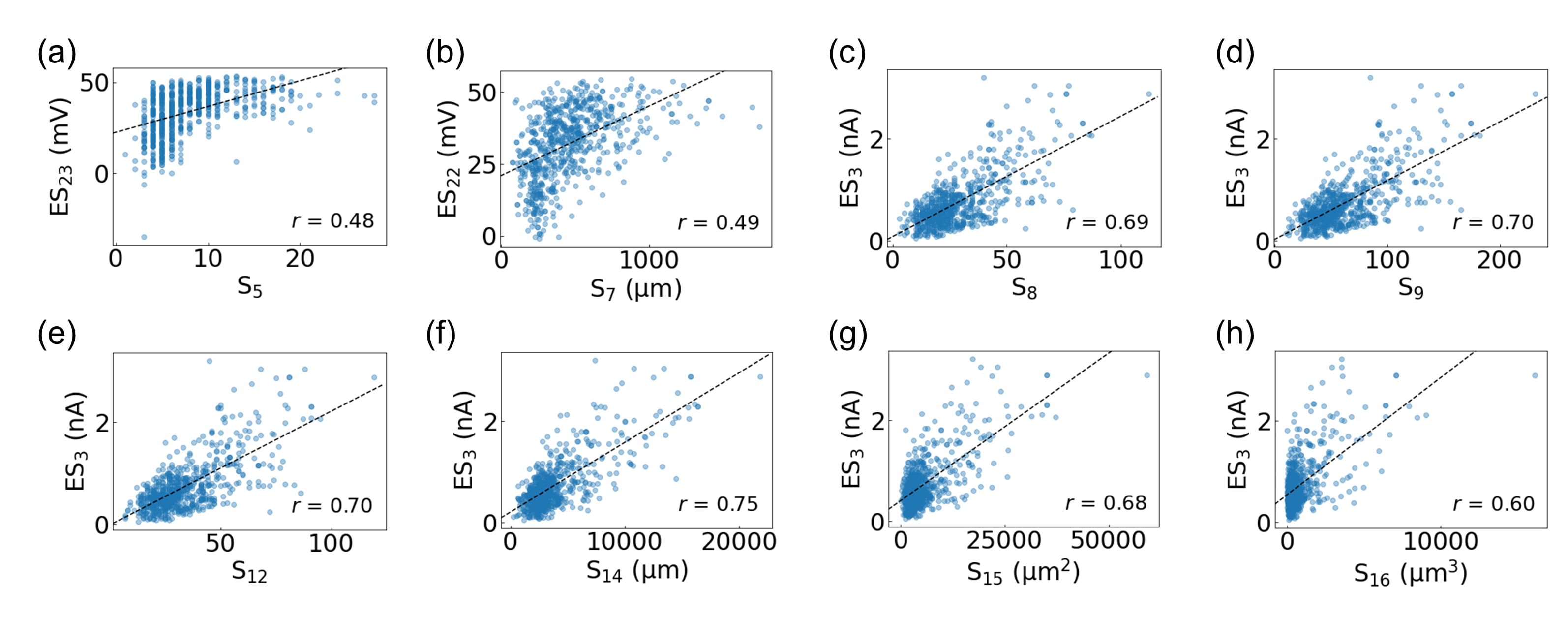Fig. 3.

Correlation analysis of the biological neurons in the Allen Cell Types Database. The most strongly correlated electrophysiological feature for each of the primary structural features is displayed: (a) S${}_5$, (b) S${}_7$, (c) S${}_8$, (d) S${}_9$, (e) S${}_{12}$, (f) S${}_{14}$, (g) S${}_{15}$, and (h) S${}_{16}$. The black dashed line denotes the trend by linear regression and r is the Pearson correlation coefficient.

The essential dynamic behaviors of the three hippocampal neurons are exhibited in Fig. 4. The long square current input for one second is fed into the soma, and the output spike train at the soma is measured. The I-f curve, which represents the relation between firing rate f and the magnitude I of the input current, is presented in the first row of Fig. 4. The I-f relations of CA1 and CA3 pyramidal neurons show similar patterns, with their maximum frequencies around 190 Hz, observed at the input current I ~ 1.26 nA and 1.03 nA for the CA1 neuron and CA3 neuron, respectively. The maximum frequency for the DG granule cell is approximately 315 Hz, much higher than pyramidal neurons. In addition, the rheobase (i.e., the minimum current amplitude that results in an action potential) value for the DG granule cell is much lower than those for the CA1 and CA3 pyramidal neurons.

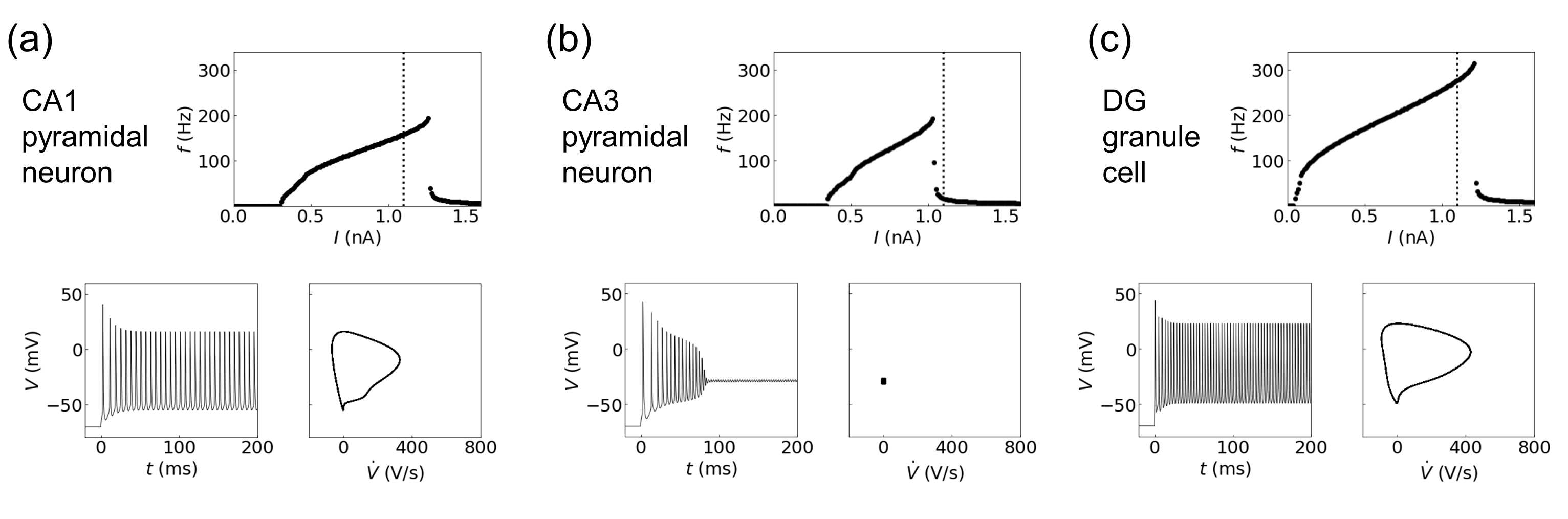Fig. 4.

Dynamics of three hippocampal neurons: (a) pyramidal neuron in CA1 and (b) pyramidal neuron in CA3, and (c) granule cell in the dentate gyrus. The first row displays the I-f curves, followed by the time evolution of output spike trains (left) and the phase portraits of steady-state dynamics (100–200 ms) on the V˙-V plane (right) in the second row.

Upon the input current I = 1.1 nA (indicated with vertical dotted line), while the CA1 neuron and DG cell show the regular spiking with a frequency of 158 Hz (for CA1 neuron) and 277 Hz (DG cell), the CA3 neuron manifests bistability at the point called the depolarization block—a silent state that occurs in every neuron when it receives excessive excitation [45]. These dynamical changes of the spike train are captured by the phase portrait of membrane potential V and its time derivative V ≡ dV/dt (right panel in the second row of Fig. 4). At I = 1.1 nA, the limit cycle attractors of CA1 neuron and DG cell reflect their regular spiking behaviors with intrinsic frequencies; CA3 neuron is at the point of transition from the regular spiking to the silent state as represented by a fixed point.

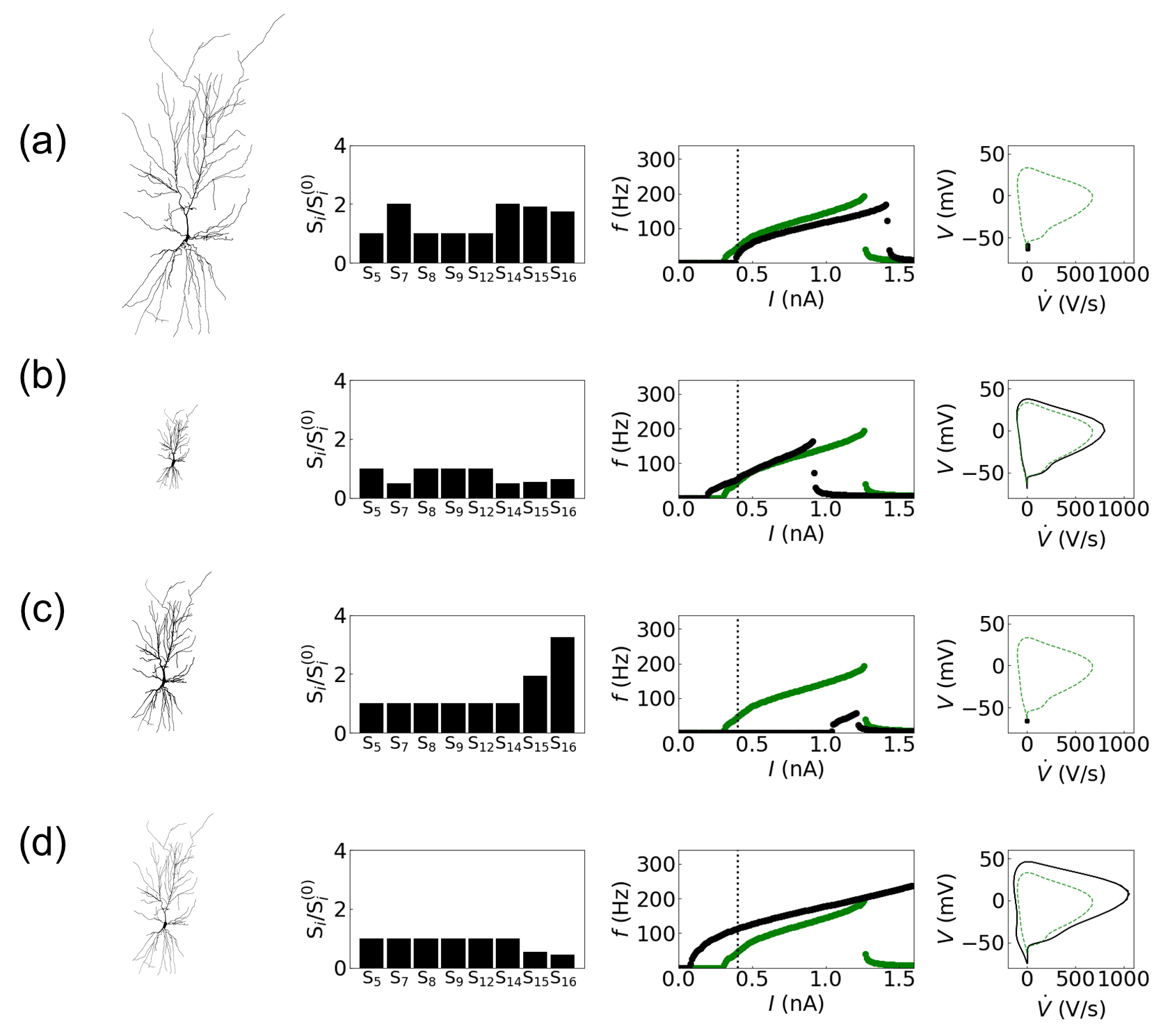Fig. 5.

Influence of structural changes in the CA1 pyramidal neuron dynamics: (a) 2-fold increase and (b) 0.5-fold decrease in the dendritic length, and (c) 2-fold increase and (d) 0.5-fold decrease in the dendritic diameter. The first column displays the modified model structures, followed by the characterization of modified structures using the primary structural features of the Allen Cell Types Database (the second column) and the I-f curves (the third column). The I-f curves of the original structure and of the modified structure are plotted in green and in black, respectively. The last column exhibits the phase portrait on the V-V˙ plane at I = 0.4 nA. The black solid line/dot and the green dashed line represent the results with and without structural changes, respectively.

Fig. 5 exhibits how structural modifications affect neural dynamics of the CA1 pyramidal neuron. The resulting neural dynamics upon the structural modifications exhibit reasonable operations. The first column of each row displays the modified structure, followed by the characterization of the structure using the primary features (S${}_{\mathrm{5}}$, S${}_{\mathrm{7}}$, S${}_{\mathrm{8}}$, S${}_{\mathrm{9}}$, S${}_{\mathrm{12}}$, S${}_{\mathrm{14}}$, S${}_{\mathrm{15}}$, S${}_{\mathrm{16}}$) of the Allen Cell Types Database (see Table 1 and Fig. 2c); the changes are presented relative to the default values before structural modifications, indicated as S${}_i$${}^{\mathrm{(}\mathrm{0}\mathrm{)}}$ for i = 5, 7, 8, 9, 12, 14, 15, and 16 (i.e., fold increase or decrease with respect to the default value, S${}_i$/S${}_i$${}^{\mathrm{(}\mathrm{0}\mathrm{)}}$). The last two columns display the I-f curve and phase portrait on the V-V˙ plane. The simulation condition has been taken the same as in Fig. 4: the output spike train is obtained at the soma upon the long square current input for one second.

When the dendritic lengths are increased by 2-fold from the total basal dendritic length of 15.76 mm (Fig. 5a), two directly related structural features ‘maximum path distance (S ${}_7$ )’ and ‘total dendritic length (S ${}_{14}$ )’ are doubled; ‘total surface area (S ${}_{15}$ )’ and ‘total volume (S ${}_{16}$ )’ exhibit ~2-fold increases. The I-f curve (the third column) moves to the right, indicating that the rheobase and the threshold current for depolarization block become higher. At a given input current (e.g., I = 0.4 nA, marked with the vertical dotted line), the neuronal firing is reduced compared to the dynamics of the original model (the green curve). In contrast, when dendritic lengths are decreased in half (i.e., S ${}_{14}$ /S ${}_{14}$ ${}^{(0)}$ = 0.5), its I-f curve is shifted to the left, indicating that the modified model can fire under smaller input currents (i.e., lower rheobase) than the normal model (Fig. 5b). The threshold current for the depolarization block is also lower than the default value. The shapes and sizes of the limit cycles of the modified structures are significantly changed from that of the normal structure (the last column of Fig. 5); this implies that the meaningful change in the spiking behavior occurs upon the modification of dendritic length.

We now compare the results of varying the dendritic lengths with those from modifications of the number of dendritic branches. Dendritic branches are added to make the total dendritic length double (Supplementary Fig. 1a in Supplementary material): a branch (156.07 $\mu$m in length, 0.5 $\mu$m in diameter) is added to each of all 101 bifurcation points, leading to a total increase of about 15.76 mm. In accord, five features related directly to the modification, ‘maximum branch order (S${}_5$)’, ‘number of bifurcations (S${}_8$)’, ‘number of branches (S${}_9$)’, ‘number of tips (S${}_{12}$)’, and ‘total dendritic length (S${}_{14}$)’ are doubled (i.e., S${}_i$ /S${}_i$${}^{(0)}$$\approx$2 for i = 5, 8, 9, 12, and 14) (the second column of Supplementary Fig. 1a). Dendritic branches are randomly removed to reduce the total dendritic length in half (i.e., S${}_{14}$ /S${}_{14}$${}^{(0)}$ $\approx$ 0.5). When the number of dendrites is increased by 2-fold, the I-f curve moves to the right (Supplementary Fig. 1a), whereas upon removing the dendritic branch the operation range is extended (i.e., the rheobase is decreased and the threshold for depolarization block is increased) (Supplementary Fig. 1b). Although the total dendritic length change is the same as the corresponding modifications of dendritic lengths without adding or removing any branches (Fig. 5a and 5b), the shapes of I-f curves are significantly different between each of the corresponding conditions (Fig. 5a and 5b): the model with 2-fold increased dendritic length (Fig. 5a) exhibits a larger operation range, exhibiting a lower rheobase and a higher threshold current for depolarization block. The model with a 0.5-fold decreased dendritic length (Fig. 5b) has a similar rheobase value as the case of deleting branches (Supplementary Fig. 1b), but the threshold current for depolarization block is much lower. It is revealed that the dendritic diameter also has a significant influence on the spike dynamics as captured by the I-f curve. Unlike previous structural modifications, increasing the diameter by 2-fold significantly lowers the maximum frequency of firing to ~ 57 Hz (Fig. 5c), and decreasing the diameter by 0.5-fold (Fig. 5d) promotes the maximum frequency to ~ 237 Hz (at I = 1.6 nA). Again, the phase portraits on the V-V˙plane manifest significantly different output spike trains between the different structural modifications. The shapes of action potentials are not changed notably upon all the structural variations (data not shown).

The detailed dynamics and information processing of the CA1 pyramidal neuron model are displayed in Fig. 6. The schematic diagram in Fig. 6a illustrates the information transfer pathway in the neuron. The hidden state triggers a synaptic input that stimulates the AMPA-type glutamate receptors of a synapse located on a dendritic spine. The resulting EPSP travels from the dendrite to the soma. The mutual information I(x; y) quantifies the total information transmitted from the hidden state to the postsynaptic spike train. The presynaptic stimulus is provided on a synapse at one of seven equidistant locations on an apical dendrite branch labeled A–G; the seven locations are 50 $\mu$m apart with distances ranging from 100 (A) to 400 $\mu$m (G) from the soma along the dendritic branch in three-dimensional space. On the right of Fig. 6a, the time evolutions of the hidden state, the conductance of the AMPA-type glutamate receptor, EPSP, and the membrane potential of the soma are shown when the presynaptic stimulus is provided at location D.

Fig. 6.

Effects of stimulus location on dynamics and information processing of the CA1 pyramidal neuron. (a) Schematic diagram of information transfer in the neuron. The path that we focused on the dendritic tree is colored in red and the locations of the synaptic input (i.e., A to G) are marked with blue dots. The dynamics of the neuron when the synapse is placed on D is shown on the right. Synaptic input triggered by the hidden state x is transmitted through the AMPA-type glutamate receptors on the spine. The stimulation changes the conductance of the receptors, which in turn evokes the excitatory postsynaptic potential (EPSP). The EPSP is propagated down from the dendrite to soma. Mutual information I(x; y) between hidden state x and spike train y at the soma is quantified. (b) Dependence of postsynaptic firing rate f on presynaptic firing rate q${}_{o\mathit{}n}$ for each location of synaptic input (i.e., A–G). The circles are colored according to the location of the stimulus as follows: black denotes location A; brown, B; pink, C; red, D; green, E; orange, F; blue, G. Error bars indicate standard error of five independent simulations. Circles for locations A–C overlap at all points. (c) Dependence of mutual information I(x; y) on q${}_{o\mathit{}n}$. (d) Dependence of f and I(x; y) on the location of the stimulus when q${}_{o\mathit{}n}$= 200 Hz. Filled and empty circles indicate f and I(x; y), respectively. In (b) and (c), circles representing frequencies and mutual information upon the stimuli at locations A, B, C overlap each other; their values are all zero because no action potentials are generated.

Fig. 6b and 6c display the firing rate and mutual information of the CA1 pyramidal neuron upon varying presynaptic firing rate q ${}_{on}$ . The minimum q ${}_{on}$ required for firing (i.e., threshold) is much lower for proximal locations such as G and F than for distal ones. The threshold values increase nonlinearly with the distance from the soma. Both the firing rate and mutual information increase in a roughly linear manner once the threshold is reached. Fig. 6d plots the postsynaptic firing rate and mutual information for varying stimulus locations at q ${}_{on}$ = 200 Hz: there are no neural activity and information transfer when the presynaptic inputs are provided at locations A to C. In contrast, the dynamics and information transfer drastically increase as the input location is moved further toward G.

The information processing of the CA1 pyramidal neuron shown in Fig. 6 can be mapped to AND/OR-like Boolean operations depending on the synaptic location. When the stimulus is given proximal to the soma (e.g., G), a low q ${}_{on}$ is sufficient to evoke the postsynaptic neuronal activity and the information transfer—this can be mapped to an OR logic gate in which only one ‘true’ input is necessary for ‘true’ output. For distal locations (D or E), a higher q ${}_{on}$ is required for the neuronal activity/information transfer, which corresponds to an AND gate that needs more than one ‘true’ input for ‘true’ output. At locations A to C, the synapse is insufficient to transfer information by itself and cannot be mapped to a logic operation within the observed q ${}_{on}$ values (0–300 Hz).

Based on the single-cell level information, we analyze the information processing of the direct and indirect hippocampal pathways consisting of CA1, CA3, and DG cells. This circuit is a computational representation of the biological two-input system of CA1 [46, 47, 48], where the CA1 pyramidal neuron can take inputs either directly or indirectly. This circuit is the primary information processing unit for match/mismatch calculation between what is encountered and what is expected—this continuous calculation is important for memory encoding and retrieval in the hippocampus [49, 50, 51]. Hidden state $x_1$ of the entorhinal cortex initiates the direct pathway of the circuit, where the input triggered by x${}_1$ is delivered to a distal region of the CA1 dendrite. Hidden state $x_2$ is a part of the indirect pathway, whereby the input propagates from DG, through CA3, to a proximal region of CA1 (Fig. 7a). Two hidden states $x_1$ and $x_2$ are coupled with the coherence $\alpha$, which is set equal to 0.1.

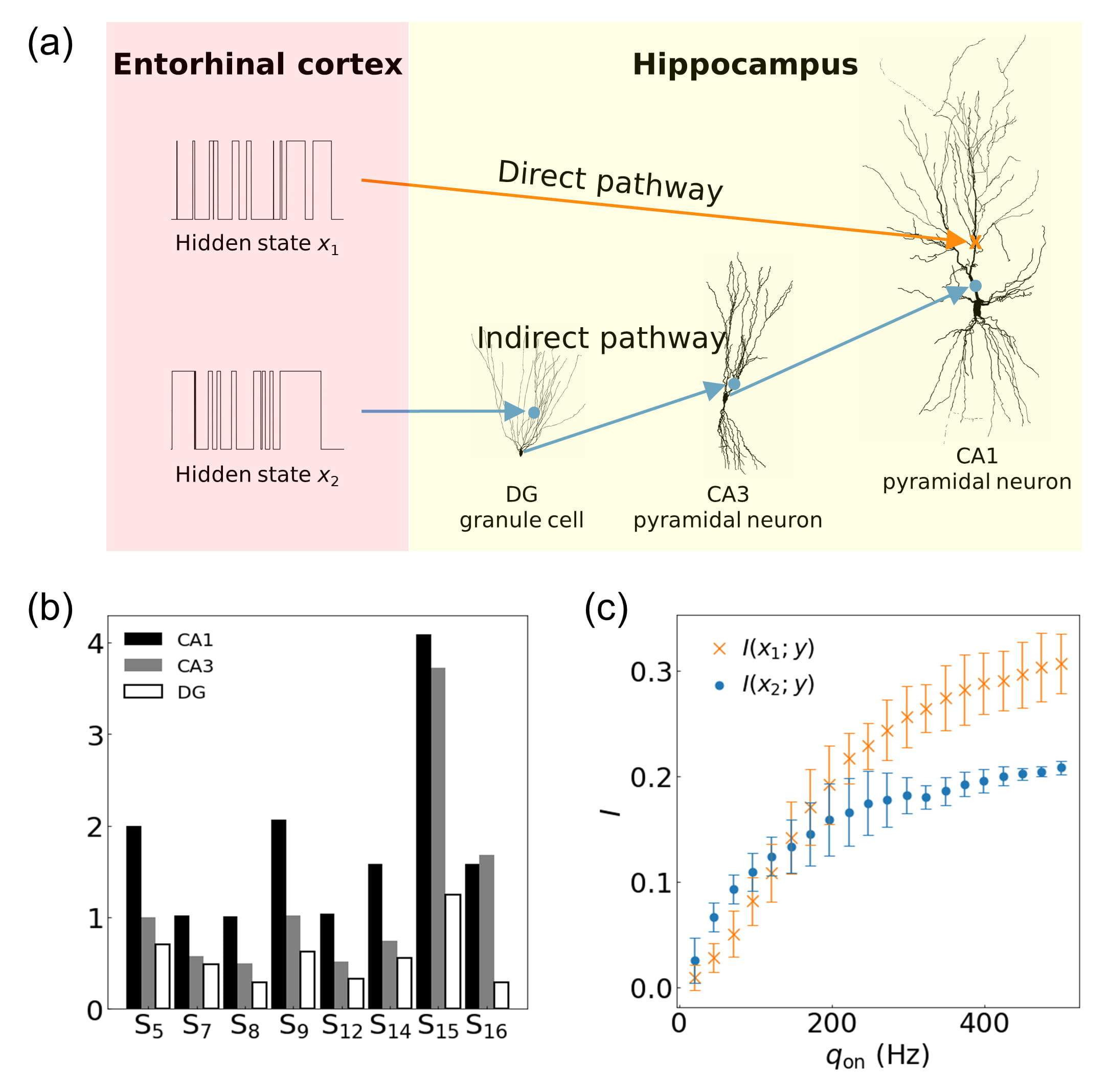Fig. 7.

Characterizations of the hippocampal direct and indirect pathways. (a) Schematic diagram of the circuit constructed using pyramidal neurons in CA1 and CA3, and a granule cell in DG. Two hidden states x${}_{\mathrm{1}}$ and x${}_{\mathrm{2}}$, coupled with a coherence $\alpha \mathrm{=}\mathrm{0.1}$, trigger synaptic inputs from the entorhinal cortex to the hippocampal neurons. The input triggered by x${}_{\mathrm{1}}$ stimulates a distal synapse located on the dendrite of the CA1 pyramidal neuron and the input triggered by x${}_{\mathrm{2}}$ stimulates the DG granule cell, which transmits the signal to the CA3 pyramidal neuron; this in turn stimulates a proximal synapse on the dendrite of CA1 pyramidal neuron. (b) Primary structural features (see Fig. 2) of the neurons in the circuit. Black, gray and white colors indicate the CA1 pyramidal neuron, CA3 pyramidal neuron, and DG granule cell, respectively. Each structural feature has its own unit: S${}_{\mathrm{5}}$, 10${}^{\mathrm{1}}$; S${}_{\mathrm{7}}$, 10${}^{\mathrm{3}}$$\mu$m; S${}_{\mathrm{8}}$, 10${}^{\mathrm{2}}$; S${}_{\mathrm{9}}$, 10${}^{\mathrm{2}}$; S${}_{\mathrm{12}}$, 10${}^{\mathrm{2}}$; S${}_{\mathrm{14}}$, 10${}^{\mathrm{4}}$$\mu$m; S${}_{\mathrm{15}}$, 10${}^{\mathrm{4}}$$\mu$m${}^{\mathrm{2}}$ and S${}_{\mathrm{16}}$, 10${}^{\mathrm{4}}$$\mu$m${}^{\mathrm{3}}$. (c) The effect of presynaptic firing rate q${}_{o\mathit{}n\mathrm{,}\text{𝑖}}$ on the mutual information I(x${}_i$; y) between the hidden state x${}_i$ and the output y of the CA1 pyramidal neuron. Orange crosses indicate mutual information of the direct pathway I(x${}_{\mathrm{1}}$; y) as a function of q${}_{o\mathit{}n\mathrm{,}\mathrm{1}}$ with q${}_{o\mathit{}n\mathrm{,}\mathrm{2}}$ fixed to 1 Hz, while blue filled circles denote the mutual information of the indirect pathway I(x${}_{\mathrm{2}}$; y) as a function of q${}_{o\mathit{}n\mathrm{,}\mathrm{2}}$ with fixed to 1 Hz. Error bars represent the standard deviations of five independent simulations.

The structural properties of the three neurons in the circuit are characterized using the eight primary structural features obtained from the Allen Cell Types Database (Fig. 7b). Most of the features are the largest for the CA1 pyramidal neuron and the smallest for the DG granule cell. However, total volume (S ${}_{16}$ ) is the largest for the CA3 pyramidal neuron, followed by the CA1 pyramidal neuron and the DG granule cell.

The dynamic ranges of mutual information of the two pathways for the firing rate are compared in Fig. 7c. Overall, both mutual information increase with the firing rate: the mutual information of the indirect pathway is higher than that of the direct pathway under a relatively lower firing rate (i.e., q ${}_{on}$ ~120 Hz), whereas they are reversed at higher firing conditions. This result from circuit analysis can be applied to optimal circuit control, as the input control is usually the most accessible parameter to modify. For example, let us consider the goal to ensure a similar level of information transfer from both the direct and indirect pathways; then the correct choice would be around I(x ${}_1$ , y) = I(x ${}_2$ , y) = 0.2, q ${}_{on,1}$ ~ 200 Hz and q ${}_{on,2}$ ~ 500 Hz.

Variations of information flow upon change of the location of synapses have been systemically examined. The location of a synapse is varied while keeping the others at the initial location (Fig. 8)—the dendritic length and dendritic diameters are fixed, while both the direct and indirect pathways are activated at the same time (q ${}_{on,1}$ = 150/q ${}_{on,2}$ = 150). For each condition, we calculate the mutual information I(x ${}_i$ , y) between x ${}_i$ (i = 1 or 2) and the output y. The mutual information increases as the synapses are located closer (proximal) to the soma, but up to an extent. The signal gets saturated, where the mutual information starts to drop afterward. We have observed a similar trend when pushing other variables to induce a stronger response. One interesting observation we make is on the proximal synapse of the CA1 pyramidal neuron, where the signal from the indirect pathway is overwhelmed by the signal from the direct pathway when the proximal synapse is too close to the soma. The locations of two synapses to CA1 have considerable influence on the overall operation of the circuit and must be finely tuned such that none of the pathways dominate the output. The structural features of each neuron can also be tuned to maximize the difference between the mutual information when only one of the pathways is turned on. For the ideal operation of the circuit, the location of two synapses must be placed optimally, which can be inferred from Fig. 8.

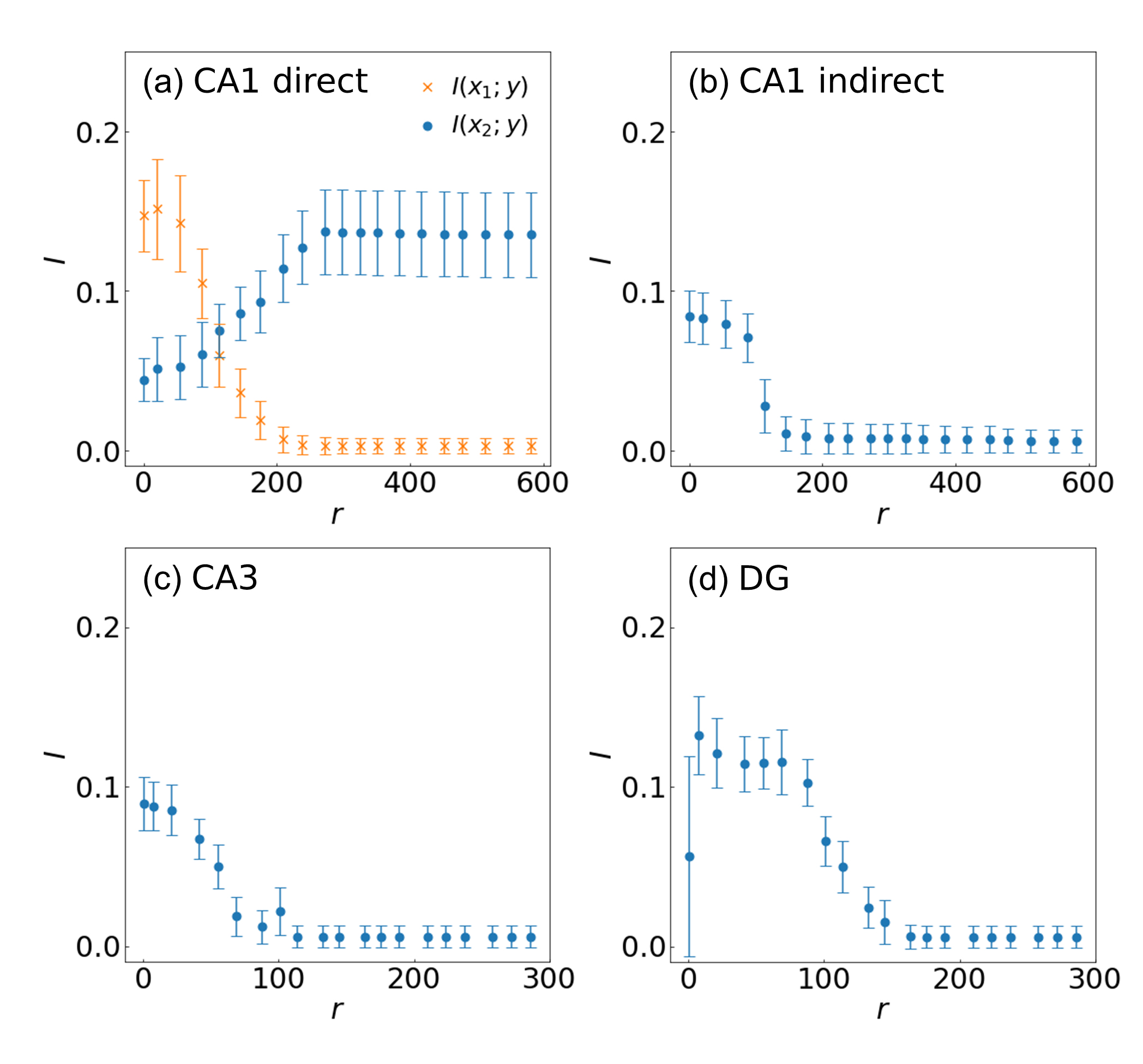Fig. 8.

Information processing of the hippocampal pathways depending on the location of synapses in the (a) CA1 pyramidal neuron receiving input from the direct pathway and (b) indirect pathway, (c) CA3 pyramidal neuron, and (d) DG granule cell. The coloring and symbols are the same as in Fig. 7. The location of the synapse is expressed as the path distance r from the soma. Firing rates q${}_{o\mathit{}n\mathrm{,}\text{𝑖}}$ (i = 1 or 2) are set to be 150 Hz. Error bars indicate standard errors for five independent simulations.

We then explore how the modification of neuronal structure can control the information processing of the direct and indirect hippocampal pathways. The mutual information increases with shorter dendritic length (L) and smaller dendritic diameter (D) (Fig. 9). Again, the primary structural features are used for describing these structural modifications. Modifying L or D has similar structural effects for all three neuron types. Four structural features, S ${}_7$ , S ${}_{14}$ , S ${}_{15}$ , and S ${}_{16}$ , have a linear relationship with L. As D increases, S ${}_{15}$ also increases linearly, while the increase of S ${}_{16}$ is proportional to D ${}^2$ . Here, either direct or indirect pathway is activated (i.e., q ${}_{on,1}$ = 150/q ${}_{on2}$ = 1 or q ${}_{on,1}$ = 1/q ${}_{on,2}$ = 150) to characterize the information processing of each pathway. In the CA1 pyramidal neuron, which is the only neuron in the circuit in the direct pathway, structural features (S ${}_7$ , S ${}_{14}$ , S ${}_{15}$ , and S ${}_{16}$ for length modification; S ${}_{15}$ and S ${}_{16}$ for diameter modification) are negatively correlated with I(x ${}_1$ ; y). For the indirect pathway, I(x ${}_2$ ; y) remains unchanged by the length modification in CA1 and CA3 pyramidal neurons. When the diameter is modified, I(x ${}_2$ ; y) shows the inverted sigmoidal shape. Exceeding certain values of S ${}_{15}$ and/or S ${}_{16}$ might induce a rapid decrease in I(x ${}_2$ ; y). Structural modifications of the DG granule cell result in a different outcome. As the length of the dendrite is increased, S ${}_7$ , S ${}_{14}$ , S ${}_{15}$ , and S ${}_{16}$ show negative correlations with I(x ${}_2$ ; y), and diameter modification of the DG granule cell makes no change in I(x ${}_2$ ; y).

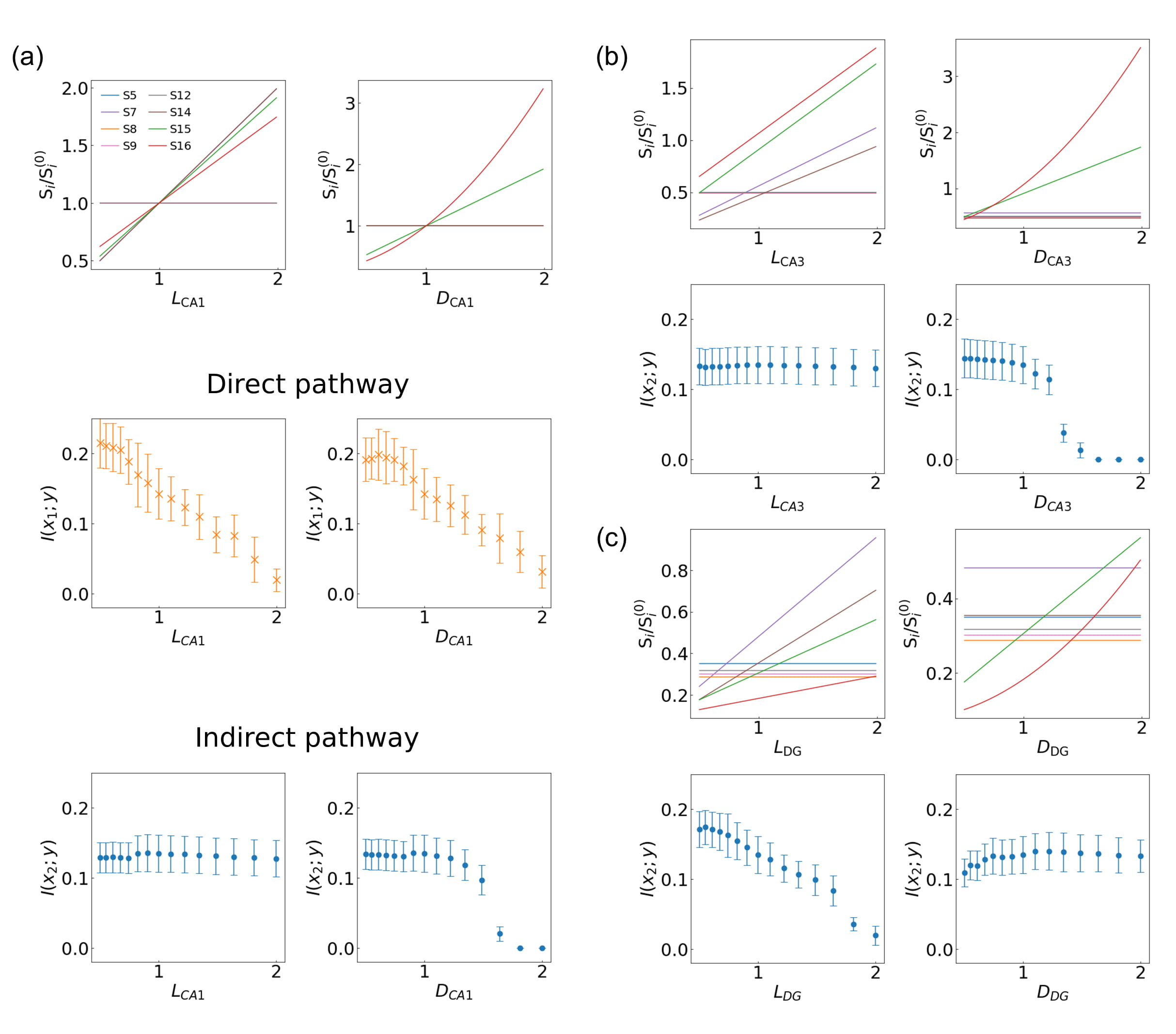Fig. 9.

Influence of structural changes of the (a) CA1 pyramidal neuron, (b) CA3 pyramidal neuron, and (c) DG granule cell on the information processing of direct and indirect hippocampal pathways. Left and right columns indicate the modification in length L${}_R$ and diameter D${}_R$ of the corresponding neuron (Subscript R denotes CA1, CA3, or DG). The top panels of each subfigure represent the eight primary structural features (see Fig. 2) changed by the structural modification. In the remaining figures, mutual information I(x${}_{\mathrm{1}}$; y) between hidden state x${}_{\mathrm{1}}$ and output y of the CA1 pyramidal neuron is marked with orange crosses and I(x${}_{\mathrm{2}}$; y) with blue-filled circles. For the simulation of I(x${}_{\mathrm{1}}$; y) or I(x${}_{\mathrm{2}}$; y), firing rates (q${}_{o\mathit{}n\mathrm{,}\mathrm{1}}$, q${}_{o\mathit{}n\mathrm{,}\mathrm{2}}$) have been taken to be (150 Hz, 1 Hz) or (1 Hz, 150 Hz). Standard errors have been calculated in five independent simulations.

We notice that the trend is not universal, as certain parts of the circuit have a very limited impact on controlling the mutual information. This is particularly recognizable when the indirect pathway is activated. Structural features such as the dendritic diameter of DG (D ${}_{DG}$ ), dendritic length of CA3 (L ${}_{CA3}$ ), and dendritic length of CA1 (L ${}_{CA1}$ ) have minimal influence on the mutual information, making these features nonoptimal targets for neural circuit control.

The results under high coherence conditions (i.e., $\alpha =0.9$) are presented in Supplementary Fig. 2 in the supplementary material. When two inputs are highly coherent, the profile of the mutual information from the indirect pathway is synchronized strongly to that of the direct pathway. Furthermore, we see a non-negligible basal level of the mutual information regardless of the input status, reducing the overall dynamic range. By comparing the results under low and high coherence conditions, we identify conditions that can be mapped to the specific Boolean logic operations. The OR operation is trivial as the CA1 neuron can transfer signals from either direct or indirect pathway and both at the same time, as long as the circuit is configured to process signals through each pathway. The AND operation emerges when signals from individual pathways are configured to be weak (e.g., both synapses to CA1 are too distal or the dendritic length and diameter are too large), but the synchronized input from both pathways starts to recover I. We also notice the possibility of the XOR-like operation by controlling the firing rate under low coherence conditions. When firing rates q${}_{on}$ from both pathways are high, the signal can get saturated and I starts to drop; this XOR-like nature may contribute to the intrinsic computational capability of the circuit, that is mismatch/match calculations for memory encoding/retrieval [49, 50, 51].